ATURAN COSINUS
Sudah disinggung sedikit sebelumnya, bahwa aturan cosinus dapat digunakan untuk menentukan panjang salah satu sisi segitiga atau besar salah satu sudut segitiga. Persamaan yang terdapat pada aturan cosinus juga diperoleh dengan memanfaatkan fungsi trigonometri dan teorema pythagoras.
Sebagai pengantar, simak cara mendapatkan tiga persamaan pada aturan cosinus di bawah.
Perhatikan gambar di bawah!
Pada 
:
:![\[ Sin \; B = \frac{h}{a} \rightarrow h = a \cdot Sin \; B \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-22c3915d10f1f614230756a7a6d46ac4_l3.png "Rendered by QuickLaTeX.com")
![\[ Cos \; B = \frac{DB}{a} \rightarrow DB = a \cdot Cos \; B \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-36befa3b73cc830f23cd50adda4016bc_l3.png "Rendered by QuickLaTeX.com")
![\[ AD = AB - DB = c - a \cdot Cos \; B \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-2c1721f1a7dfbca602a7d9392604d614_l3.png "Rendered by QuickLaTeX.com")
Pada 
dapat diperoleh persamaan di bawah (berdasar teorema pythagoras):
dapat diperoleh persamaan di bawah (berdasar teorema pythagoras):![\[ AC^{2} = AD^{2} + CD^{2} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-572546634701ecbea23e973547df5300_l3.png "Rendered by QuickLaTeX.com")
![\[ b^{2} = \left( c - a \cdot Cos \; B \right)^{2} + \left( a \cdot Sin \; B\right)^{2} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-f40a6186aa5af698e64195ef3fe225be_l3.png "Rendered by QuickLaTeX.com")
![\[ b^{2} = c^{2} - 2ac \cdot Cos \; B + a^{2} \cdot Cos^{2}B + a^{2} \cdot Sin^{2} B \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-636cbb28ba72e3fadc3effe5d88a6d7c_l3.png "Rendered by QuickLaTeX.com")
![\[ b^{2} = c^{2} - 2ac \cdot Cos \; B + a^{2} \left( Cos^{2}B + Sin^{2} B\right) \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-1de35bfd57e4c5c2f82befc91cc621c2_l3.png "Rendered by QuickLaTeX.com")
![\[ b^{2} = c^{2} - 2ac \cdot Cos \; B + a^{2} \cdot 1 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-4eaf58fc15eceb92bfd5a0591185ee0c_l3.png "Rendered by QuickLaTeX.com")
![\[ b^{2} = c^{2} - 2ac \cdot Cos \; B + a^{2} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-369cdf3af26470cda8a05ad46469e2bd_l3.png "Rendered by QuickLaTeX.com")
![\[ b^{2} = c^{2} + a^{2} - 2ac \cdot Cos \; B \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-8833364312b0d0d3e1ae453bea05b597_l3.png "Rendered by QuickLaTeX.com")
Persamaan akhir yang di atas merupakan salah satu aturan cosinus. Dengan mengikuti langkah serupa seperti yang telah dikerjakan di atas, akan diperoleh tiga buah persamaan aturan cosuinus. Tiga buah persamaan tersebut dapat dilihat pada gambar di bawah.
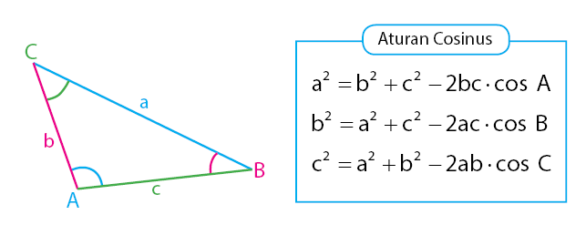
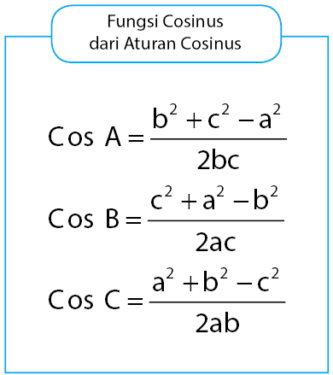
Berdasarkan tiga persamaan aturan cosinus di atas, dapat diperoleh rumus fungsi cosinus yang dapat digunakan untuk menentukan besar sudut segitiga jika diketahui panjang ketiga sisi segitiga. Persamaan fungsi cosinus tersebut dapat dilihat pada persamaan di bawah.
Contoh Soal dan Pembahasan
Pada suatu segitiga dengan sisi-sisi a, b, dan c memenuhi 
. Maka besar sudut A adalah ….
A.
B.
C.
D.
E.
. Maka besar sudut A adalah ….A.
B.
C.
D.
E.
Pembahasan:
Diketahui:
![\[ a^{2} - b^{2} = c^{2} - bc\]](https://idschool.net/wp-content/ql-cache/quicklatex.com-77b8fe5752f0f34041dddfea45dd4072_l3.png "Rendered by QuickLaTeX.com")
Sehingga,
![\[ a^{2} = b^{2} + c^{2} - bc \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-8c12e5aeacdea0f65128a910ede1ce00_l3.png "Rendered by QuickLaTeX.com")
Salah satu rumus cosinus adalah:
![\[ a^{2} = b^{2} + c^{2} - 2bc \cdot cos \; A \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-75c688c4ab11bb5e3ff68ef6fc1e7f32_l3.png "Rendered by QuickLaTeX.com")
Berdasarkan dua persamaan di atas, akan diperoleh nilai cos A.
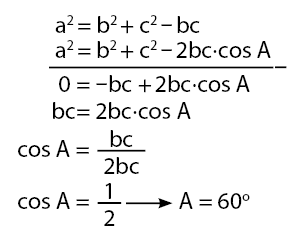
Post a Comment