Identitas Trigonometri
Dalam suatu segitiga siku-siku, selalu berlaku prinsip phytagoras, yaitu  . Pada materi ini, prinsip phytagoras ini menjadi asal pembuktian identitas trigonometri sendiri.
. Pada materi ini, prinsip phytagoras ini menjadi asal pembuktian identitas trigonometri sendiri.
 bagi kedua ruas dengan
bagi kedua ruas dengan 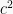 , diperoleh persamaan baru
, diperoleh persamaan baru  . Sederhanakan dengan sifat eksponensial menjadi
. Sederhanakan dengan sifat eksponensial menjadi  . Dari persamaan terakhir, subtitusi bagian yang sesuai dengan perbandingan trigonometri pada segitiga, yaitu
. Dari persamaan terakhir, subtitusi bagian yang sesuai dengan perbandingan trigonometri pada segitiga, yaitu  dan
dan  , sehingga diperoleh
, sehingga diperoleh  atau bisa ditulis menjadi
atau bisa ditulis menjadi  .
.
Dari identitas yang pertama, dapat diperoleh bentuk lainnya, yaitu:
 bagi kedua ruas dengan
bagi kedua ruas dengan  , diperoleh
, diperoleh  dimana
dimana  dan
dan 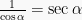 , sehingga diperoleh:
, sehingga diperoleh: 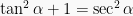
Bentuk ketiga yaitu  dibagi dengan
dibagi dengan 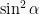 menjadi
menjadi 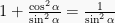 , dimana
, dimana  dan
dan  , sehingga diperoleh persamaan:
, sehingga diperoleh persamaan: 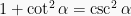 .
.
Contoh Soal Trigonometri
Tentukanlah nilai dari sin 1200 + cos 2100 + cos 3150
Jawab:
 berada pada kuadran 2, sehingga nilainya tetap positif dengan besar sama seperti
berada pada kuadran 2, sehingga nilainya tetap positif dengan besar sama seperti 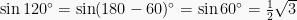
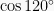 berada pada kuadran 3, sehingga nilainya negatif dengan besar sama seperti
berada pada kuadran 3, sehingga nilainya negatif dengan besar sama seperti 
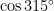 berada pada kuadran 4, sehingga nilainya positif dengan besar sama seperti
berada pada kuadran 4, sehingga nilainya positif dengan besar sama seperti 
Jadi


 . Pada materi ini, prinsip phytagoras ini menjadi asal pembuktian identitas trigonometri sendiri.
. Pada materi ini, prinsip phytagoras ini menjadi asal pembuktian identitas trigonometri sendiri. dibagi dengan
dibagi dengan 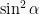 menjadi
menjadi 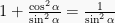 , dimana
, dimana  dan
dan  , sehingga diperoleh persamaan:
, sehingga diperoleh persamaan: 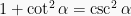 .
.


Post a Comment