ATURAN SINUS
Aturan sinus merupakan persamaan yang menyatakan hubungan tiga sudut dan tiga sisi yang terdapat pada segitiga sembarang. Tujuan dari penggunaan aturan sinus adalah untuk mengetahui panjang sisi segitiga yang terdapat pada segitiga sembarang. Atau dapat juga digunakan untuk mengetahui besar sudut segitiga yang belum diketahui.
Sebelumnya, sobat idschool sepertinya perlu tahu dari mana persamaan sinus diperoleh. Simak cara mendapatkan persamaan aturan sinus yang akan diberikan di bawah.
Perhatikan gambar di bawah!

Pada  :
:
Pada  :
:
Berdasarkan dua persamaan di atas, dapat disimpulkan bahwa
Dengan cara yang serupa akan diperoleh persamaan aturan sinus seperti yang diberikan pada persamaan di bawah.
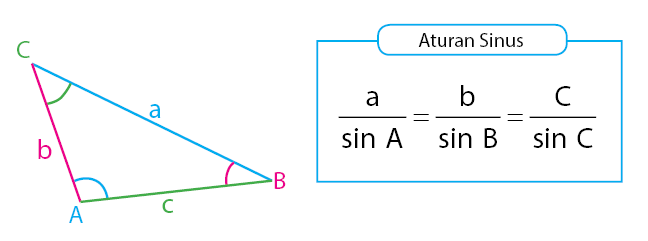
Fungsi aturan sinus di atas dapat digunakan untuk menentukan panjang sisi segitiga yang belum diketahui. Selain itu, juga dapat digunakan untuk mencari besar sudut segitiga yang belum diketahui.
Untuk menambah pemahaman sobat idschool, akan diberikan contoh soal yang dilengkapi dengan pembahasan mengenai penggunaan aturan sinus untuk menentukan panjang salah satu sisi segi tiga yang belum diketahui. Simak contoh soal dan pembahasan aturan sinus yang diberikan di bawah.
Contoh Soal dan Pembahasan
Suatu segitiga ABC memiliki panjang AC = 8 cm. Jika besar  dan
dan  , maka panjang BC = … cm.
, maka panjang BC = … cm.
Pembahasan:
Berdasarkan informasi yang diberikan pada soal, dapat diperoleh informasi seperti berikut ini.
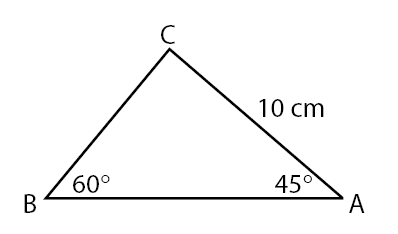
Panjang BC dapat dicari menggunakan aturan sinus.
Jawaban: E



Post a Comment